Simulating a Coin Toss with Arbitrary Bias Using Another Coin of Unknown Bias
Back in January this year I was commuting to work and routinely opened the daily coding problem email: “Good morning! Here’s your coding interview problem for today. […] Assume you have access to a function toss_biased() which returns 0 or 1 with a probability that’s not 50-50 (but also not 0-100 or 100-0). You do not know the bias of the coin. Write a function to simulate an unbiased coin toss.”
As it turned out, this problem posed a much greater challenge than I expected it to. It took me about two more commutes and quite a few Jupyter Notebook cells to come up with a first solution. An admittedly very slow and inefficient one, relying on some deep tree structures and so on. Meanwhile, I have spent some more time on the problem, did some research, and can confidently say that in this year’s birthday post I present a clear and efficient solution to a more generalized version of the coding problem.
Problem Statement
Let us start by understanding exactly what we want to do here. Suppose somebody gave you a coin with some bias. Instead of landing on heads 50% and on tails 50% of the time it has some different probabilities for heads and tails, which are unknown to you. It might for instance land heads-up in 99% of all tosses. Your task is, to simulate another unbiased coin using only the first, biased coin that is provided to you. Simulating in a sense that somebody asks you to say “heads” or “tails” and you have to reply 50-50 with either, randomly. Now that’s what the coding problem asked us to do, we will, however, take this one step further and simulate a coin of any arbitrary bias using only the first coin. The remainder of this article is combining the mathematical side of the problem with a Python implementation and verbal explanations.
The verbose, verbal formulation from above can be expressed more concisely, where $\operatorname{Ber}\left(\cdot\right)$ is the Bernoulli distribution:
Derive $Y\sim\operatorname{Ber}\left(p_2\right)$ for any $p_2\in\left[0,1\right]$, given $X\sim\operatorname{Ber}\left(p_1\right)$ with unknown $p_1\in(0,1)$.
In Python one could define a random variable following a Bernoulli distribution as a function mapping from nothing to either 0 or 1. The type is:
RandomVariable = Callable[[], int]
Next we define a higher-order function which creates random variables with any given bias. It is our biased coin generator.
def any_x_rv(p_1: float = 0.5) -> RandomVariable:
"""Returns a function that follows Ber(p_1)"""
return lambda: 1 if random.uniform(0, 1) <= p_1 else 0
Given some $p_1$, any_x_rv returns a function which, when called, returns 1 with probability $p_1$ and 0 with probability $(1-p_1)$.
We are seeking for a function
def any_y_rv(x_rv: RandomVariable, p_2: float) -> RandomVariable:
pass
which takes a random variable (e.g. some function returned by any_x_rv) and a second probability $p_2$. Note that any_y_rv does not know about the internals of x_rv. It can only evaluate the provided function. The return type of any_y_rv is again a random variable, i.e. a function that can be evaluated. It is supposed to return 1 with a probability of $p_2$.
If you want to solve the problem by yourself, now is a good time to pause and ponder. Try to implement any_y_rv!
We will tackle the problem in two steps: First, creating a fair coin from the coin that is given to us. Second, using the simulated fair coin to simulate any biased coin.
Simulating a Fair Coin with a Biased Coin
In the first step we construct a random variable $Z$ which follows $\operatorname{Ber}\left(0.5\right)$ from $X$. Recall that $\Pr\left[X=1\right]=p_1$ is unknown to us. Let $(X_1,X_2)$ be a random sample of $X$. The probabilities for all possible outcomes of the tuple are:
$$
\begin{align}
\Pr\left[X_1=0,X_2=0\right]&=\left(1-p_1\right)^2\\
\Pr\left[X_1=0,X_2=1\right]&=\left(1-p_1\right)\times p_1\\
\Pr\left[X_1=1,X_2=0\right]&=p_1\times\left(1-p_1\right)\\
\Pr\left[X_1=1,X_2=1\right]&=p_1^2,.
\end{align}
$$
It is apparent that the probabilities for two of the four outcomes are equal, namely the ones where $X_1\ne X_2$, i.e. $\Pr\left[X_1=0,X_2=1\right]=\Pr\left[X_1=1,X_2=0\right]$. That fact comes in useful when constructing a fair coin. We define $Z$ to be 1 if $X_1=1,X_2=0$ and 0 if $X_1=0,X_2=1$. In all other cases, we draw from the tuple $(X_1,X_2)$ again. Since $X$ is non-deterministic, it is not always 0 or always 1, we are guaranteed to encounter the first case eventually.
This idea was presented by John von Neumann in “Various techniques used in connection with random digits” (1951). Verbally, the instructions are:
- Toss the biased coin two times.
- If the two outcomes are identical, ignore them and go back to step (1).
- If the two outcomes differ, use the outcome of the first coin as the result of the fair coin toss.
The Python implementation of the algorithm looks as follows:
def z_rv(x_rv: RandomVariable) -> int:
"""Returns Z~Ber(0.5)"""
while True:
x_1, x_2 = x_rv(), x_rv()
if x_1 != x_2:
return x_1
The function z_rv represents $Z$. It takes another random variable $X$, which represents the biased coin. The function samples from $X$ until a sample tuple differs. Once that is the case, it returns the first element of the tuple, namely x_1.
At this point we have access to a simulated fair coin which is based on any coin with bias. In order to toss it we simply call z_rv. Time for the second step.
Simulating a Coin with Any Bias Given a Fair Coin
Given the fair coin $Z\sim\operatorname{Ber}\left(0.5\right)$, we seek to simulate $Y\sim\operatorname{Ber}\left(p_2\right)$ for any $p_2$ using $Z$. The method propounded in this section is taken from the blog post "Arbitrarily biasing a coin in 2 expected tosses" by Александър Макелов.
We start by defining the binary expansion $a_i\in\left\{0,1\right\}$, with $i\in\mathbb{N}$, of the provided probability $p_2$ as $$p_2=\sum_{i=1}^\infty\frac{a_i}{2^i}\,.$$ You can think of the values $a_1,a_2,\dots$ as the fractional digits of the binary representation of $p_2$: $p_2=0.a_1a_2\dots$. Since $p_2$ is given, the sequence is entirely known to us. Here is an example: Suppose $p_2=0.8$. It can be expressed as$$p_2=0.8=\frac{1}{2}+\frac{1}{4}+\frac{0}{8}+\frac{0}{16}+\frac{1}{32}+\dots\,,$$where $a=(1,1,0,0,1,\dots)$. $a$ can be infinite and periodic, but neither matters to us.
$a$ is implemented as a Python function returning a generator so that the infinite stream of values can be read sequentially, on demand:
def a(p: float) -> Iterable[int]:
while True:
yield 1 if p >= 0.5 else 0
p = 2 * p - int(2 * p)
Let $Z_1,Z_2,\dots$ be a random sample of $Z$. We define $$ \hat{Y}(i):=\begin{cases} 0&{\text{if }}Z\_i > a\_i\\ 1&{\text{if }}Z\_i < a\_i\\ \hat{Y}(i+1)&{\text{otherwise},} \end{cases} $$ which iterates over the fractional digits of $p_2$ and uses the $i$-th sample of $Z$ for each of them. At every step it compares $Z_i$ to the digit $a_i$ and terminates if $Z_i\ne a_i$. This blog post by Alex Irpan provides a nice visual intuition for why this works. Now $Y$ can be defined as $Y:=\hat{Y}(1)$.
In our implementation, $Y$ is a function that uses the two previously defined functions z_rv (the unbiased coin simulator) and a (the binary expansion of $p_2$):
def y_rv() -> int:
for a_i in a():
if z_rv() != a_i:
return a_i
Final Solution
Bringing the pieces together we get the following Python snippet:
import random
from typing import Callable, Iterable
RandomVariable = Callable[[], int]
def any_x_rv(p_1: float = 0.5) -> RandomVariable:
"""Returns a function that follows Ber(p_1)"""
assert 0 < p_1 < 1
return lambda: 1 if random.uniform(0, 1) <= p_1 else 0
def any_y_rv(x_rv: RandomVariable, p_2: float) -> RandomVariable:
"""Returns a function that follows Ber(p_2), based on x_rv"""
assert 0 <= p_2 <= 1
if p_2 == 0 or p_2 == 1: return lambda: p_2
def a() -> Iterable[int]:
p = p_2
while True:
yield 1 if p >= 0.5 else 0
p = 2 * p - int(2 * p)
def z_rv() -> int:
"""Returns Z~B(1,0.5)"""
while True:
x_1, x_2 = x_rv(), x_rv()
if x_1 != x_2:
return x_1
def y_rv() -> int:
for a_i in a():
if z_rv() != a_i:
return a_i
return y_rv
We can create a new, biased coin $X$, for instance with $p_1=0.1$ (this could be anything $\in(0,1)$)
>>> x_rv = any_x_rv(0.1)
and retrieve a new, biased coin $Y$ with some different bias, say $p_2=0.73$
>>> y_rv = any_y_rv(x_rv, 0.73)
just to toss it 20 times:
>>> [y_rv() for _ in range(20)]
[0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1]
And there we go: We have constructed a coin with an arbitrary bias based on another coin with unknown bias! Now it can be tossed:
A big thank you goes to my colleague Lennart van der Goten for showing a ton of interest in the problem and solving it mathematically in an entirely different, yet elegant way. My fellow student Tanja Bien took the photos for this post which look gorgeous. Thank you very much as well!
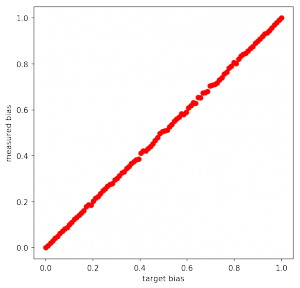
To evaluate whether the correctness of the solution, I simulated a coin for any $p_2\in\left[0,1\right]$ and tossed it many times:
import numpy as np
import matplotlib.pyplot as plt
def determine_bias(biased_fn: Callable[[], int], n: int = 10000) -> float:
"""Determines p_1 of a biased function"""
assert n > 0
return sum([biased_fn() for _ in range(n)]) / n
p_1 = 0.1
x_rv = any_x_rv(p_1)
p_2s = np.linspace(0,1,100)
ys = [determine_bias(any_y_rv(x_rv, p_2)) for p_2 in p_2s]
plt.plot(p_2s, ys, 'ro')