MOV is Turing-Complete: 4-bit Adder Implementation
In late 2017, small groups of our class were given the task to delve into the assembly language and write a program for the 8051 microcontroller, as part of the Low-Level Programming lecture. This post documents the project MOV is Turing-Complete: 4-bit Adder Implementation — an assembly program that adds two 4-bit numbers relying solely on mov instructions. The appendix lists the minified version of the code.
Authors: Timo I. Denk, Samed Güner, Tobias Robl
Baden-Württemberg Cooperative State University Karlsruhe
Supervisor: Prof. Dr. Ralph Lausen
Date of publication: 12. Dec 2017
1 Introduction
In general a variety of commands is used to write an assembly program. One can use a whole instruction set of microcontroller-specific functions. As part of the lecture Low-level programming, an assembly program capable of adding two integral numbers, will be developed; relying solely on the instructions MOV and MOVX.
The underlying microcontroller is an Intel 8051 out of the MCS-51 family, with originally 128 bytes of internal RAM and 64kB of program and data storage.
For ease of reducing setup overhead, the MCU 8051 IDE is used to simulate both the microcontroller and external hardware.
The instruction MOV operand1, operand2 copies the value of operand2 into operand1, with operand2 staying untouched. While operand2 can be a constant or an address, operand1 is the destination and has to be a memory address. Indirect addressing is accomplished using the prefix @ right before an address. That way, data is not stored at the given address but at the address which is stored by-value in the pre-fixed operand. The 8051 supports indirect addressing for the registers R0 and R1.
2 Concept
The concept of this project is based on the paper mov is Turing-complete, which was published in 2013 by Stephen Dolan at the University of Cambridge. He shows that the MOV instruction is Turing-complete.
A system of data manipulation rules such as the mov-command in the Intel 8051 is specified as Turing-complete, if it has the capability of simulating a Turing machine. The Turing machine was invented by Alan Turing in 1936 and represents one of the fundamental concepts in computer science. It is based on the conceptual experiment of Alan Turing to recreate the human thinking in numerical calculations.
A calculation in the Turning machine consists of step-by-step manipulations of symbols that are written to and read from a memory tape, according to certain rules. Chains of these symbols can be interpreted in different ways, for example as numbers. That way, a Turing machine can execute a function where the arguments (initially on the tape) are mapped to an output (sequence of symbols that are on the tape after processing by the Turing machine). A Turing machine is capable of reproducing any numerical calculations respectively all intuitively computable functions as the Church-Turing thesis manifests:
The class of Turing computable functions corresponds to the class of intuitively computable functions.
Equivalently, the Church-Turing thesis states that a computable function is computable iff it has an algorithm, so a human being can also compute it. This means all algorithms such as calculating the sum of two 4-bit integers, calculating prime numbers, or sorting a list, can be run on a Turing machine. Any other computational model, programming language, or mechanical device, with relatively enough time and resources, is capable of simulating a Turing machine and hence able to run any algorithm.
In his paper, Stephen Dolan shows the Turing-completeness of the MOV instruction. Stephen Dolan refers in his paper to branching as “the fundamental aspect of computing” and shows that the MOV-instruction can indeed be used to compare two registers.
One can compare two registers using only load and store instructions. Loading a value into address A and a different value into address B, then reading the content of the address A will show whether A and B are equal. Stephen Dolan shows how to compare two registers ($R_i$, $R_j$) as follows (where [R] denotes indirect addressing, i.e. writing/reading from the address that is stored in R):
MOV [R_i], 0 MOV [R_j], 1 MOV R_k, [R_i]
If $R_i = R_j$, $R_k$ is set to 1, otherwise it is 0. These three simple instructions represents the comparison-capability of the MOV-instruction in an elegant way.
Beside the ability to compare two registers, the MOV-instruction can be used to write band symbols onto the band, as required to simulate a Turing machine.
3 Software Implementation
Due to the lack of jump- and conditional-instructions, the entire program is a sequence of MOV and MOVX instructions, of which every single one will be executed. The last instruction is the inevitable exception to the MOV-only-constraint: It is a long jump back to the top (LJMP 0x09). It can, however, be seen as equivalent to MOV PC, #0x09 which sets the program counter register PC to the desired address.
The clutter of MOV instructions can be split into semantic parts. This section goes through each of these in detail and explains how it serves the objective of adding two 4-bit numbers and outputting the result. Table 1 lists the usage of the noteworthy registers.
| Register | Purpose |
|---|---|
| R0 | Indirect addressing of external memory |
| R1 | Indirect addressing of external memory |
| R2 | Addition finished flag |
| R3 | Integral value $a\in [0,15]$ (non-immutable) |
| R4 | Integral value $b\in [0,15]$ (non-immutable) |
| R5 | Integral value $\min (a+b, 15)$, after addition is finished |
| P1 | 7-segment output, after addition is finished |
| Table 1: Usage of notable registers. |
3.1 Initialization
The first four lines of code store the two terms of the sum in R3 and R4. Furthermore, R5 is reset to the constant #0x00. It will later, after the addition is finished, hold the sum of R3 and R4. Both, R3 and R4 will be changed during execution and wont hold their initial values.
Finally, the stack pointer SP is set to #0x2F because the general purpose section of the 8051’s RAM starts at #0x30. The stack pointer is not in use in the final, minified code version but was needed at earlier stages where subroutines were used for the purpose of simplification.
The initialization part consists of four MOV instructions.
3.2 Addition Finished Flag
After initialization, the program checks whether the value of R4 equals the constant #0x00. If true, addition is finished and the finished flag is set. That is, R2 is set to #0x01.
The finish flag is not necessarily needed, since comparing it to #0x01 is equivalent to checking R4 for inequality with #0x00. Nevertheless, it was introduced to make the check more convenient.
The addition finished part consists of seven MOV and three MOVX instructions.
3.3 Addition Result Storage
After the addition is finished, the sum of the two 4-bit numbers is stored in R5. This part of the program moves R3 to R5, if the addition finished flag in R2 is set. Otherwise, R5 is left at its initial value.
3.4 Addition Result Output
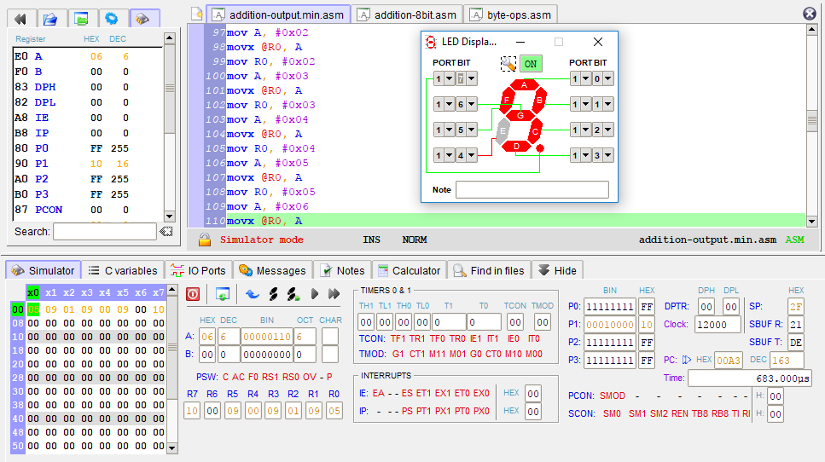
After the addition is finished, the result is shown on a 7-segment display attached to port 1. Numbers from 0 to 15 are shown in hexadecimal encoding, e.g. 10 is shown as an A. Whether or not addition is finished is determined by reading the addition finished flag in R2. If it is set, the 7-segment encoded version of the sum is being loaded and moved to P1. The former is achieved by filling the external memory temporarily with a translation table. For example, the address 0x00 stores #01000000B which corresponds to the 7-segment display code for 0. Subsequently, a look-up is performed with movx A, @R1, where R1 holds the sum. After running this instruction, A contains the code that corresponds to the value in R1, which is then used to update the output port (given that the addition finished flag is set).
The addition result output section consists of 42 MOV and 20 MOVX instructions. This gives 62 in total of which 48 serve the purpose of filling the 7-segment code look-up table.
3.5 Term of the Sum Increment
At each iteration, the first term of the sum — stored in R3 — is incremented by one, unless addition is finished. The increment works, similar to the 7-segment code, with a look-up table in the 8051’s external memory. It is filled from address 0x00 to 0x0F with the values that corresponds to the incremented address. That means 0x00 stores #0x01, 0x01 stores #0x02, and so on. Overflows are simply clipped, which means 0x0F = #0x0F.
The increment section consists of 42 MOV and 20 MOVX instructions. This gives 62 in total of which 48 serve the purpose of filling the increment look-up table.
3.6 Term of the Sum Decrement
Equivalent to the increment, the other part of the sum — stored in R4 — is decremented by one, unless the addition is finished. An underflow is not specially treated.
The decrement section consists of 42 MOV and 20 MOVX instructions. This gives 62 in total of which 48 serve the purpose of filling the decrement look-up table.
4 Conclusion
Following the theoretical work of Dolan (2013), we have shown that MOV is not only Turing-complete in theory, but also in practice. We have implemented a 4-bit adder, relying solely on MOV and MOVX instructions (with the exception of a single LJMP), on the popular Intel 8051 microcontroller. The 8051 is distinct from a normal Turing machine in several regards. Most notably, the memory is finite and split into segments of 8 bits. With bit-wise manipulation instructions such as setb (set bit) and clrb (clear bit) at hand, the undertaking would have been a lot easier.
The lack of jump instructions makes a MOV-only program extremely inefficient. At each iteration every single instruction of the program is executed, no matter whether its result is required or not. In our case, the conversion from 4-bit number to 7-segment display output is done prior to every single decrement, despite being needed only once. We did not see any chance of gaining performance by using a single instruction. Nevertheless, conducting empirical experiments on the usability of MOV-only programs is interesting and we can draw the conclusion that MOV is sufficient to solve simple tasks.
References
- Stephen Dolan. _
MOVis Turing-complete. _Computer Laboratory, University of Cambridge, 2013.
https://www.cl.cam.ac.uk/~sd601/papers/mov.pdf
A Source Code
The following source code is the basis of this article. Relying solely on MOV instructions, it iteratively adds the values stored in R3 and R4, and writes the sum to R5. Furthermore, it shows the computed sum at a 7-segment display attached to P1.
0000 7B04 mov R3, #0x04 ; A 0002 7C03 mov R4, #0x03 ; B 0004 7D00 mov R5, #0x00 ; A + B 0006 75812F mov SP, #0x2F 0009 EA mov A, R2 000A 7800 mov R0, #0x00 000C F2 movx @R0, A 000D EC mov A, R4 000E F8 mov R0, A 000F 7401 mov A, #0x01 0011 F2 movx @R0, A 0012 7800 mov R0, #0x00 0014 E2 movx A, @R0 0015 FA mov R2, A 0016 ED mov A, R5 0017 7801 mov R0, #0x01 0019 F2 movx @R0, A 001A EA mov A, R2 001B F8 mov R0, A 001C EB mov A, R3 001D F2 movx @R0, A 001E 7801 mov R0, #0x01 0020 E2 movx A, @R0 0021 FD mov R5, A 0022 ED mov A, R5 0023 F9 mov R1, A 0024 7440 mov A, #01000000B 0026 7800 mov R0, #0x00 0028 F2 movx @R0, A 0029 7479 mov A, #01111001B 002B 7801 mov R0, #0x01 002D F2 movx @R0, A 002E 7424 mov A, #00100100B 0030 7802 mov R0, #0x02 0032 F2 movx @R0, A 0033 7430 mov A, #00110000B 0035 7803 mov R0, #0x03 0037 F2 movx @R0, A 0038 7419 mov A, #00011001B 003A 7804 mov R0, #0x04 003C F2 movx @R0, A 003D 7412 mov A, #00010010B 003F 7805 mov R0, #0x05 0041 F2 movx @R0, A 0042 7402 mov A, #00000010B 0044 7806 mov R0, #0x06 0046 F2 movx @R0, A 0047 7478 mov A, #01111000B 0049 7807 mov R0, #0x07 004B F2 movx @R0, A 004C 7400 mov A, #00000000B 004E 7808 mov R0, #0x08 0050 F2 movx @R0, A 0051 7410 mov A, #00010000B 0053 7809 mov R0, #0x09 0055 F2 movx @R0, A 0056 7408 mov A, #00001000B 0058 780A mov R0, #0x0A 005A F2 movx @R0, A 005B 7403 mov A, #00000011B 005D 780B mov R0, #0x0B 005F F2 movx @R0, A 0060 7446 mov A, #01000110B 0062 780C mov R0, #0x0C 0064 F2 movx @R0, A 0065 7421 mov A, #00100001B 0067 780D mov R0, #0x0D 0069 F2 movx @R0, A 006A 7406 mov A, #00000110B 006C 780E mov R0, #0x0E 006E F2 movx @R0, A 006F 740E mov A, #00001110B 0071 780F mov R0, #0x0F 0073 F2 movx @R0, A 0074 E3 movx A, @R1 0075 FF mov R7, A 0076 74FF mov A, #0xFF 0078 7801 mov R0, #0x01 007A F2 movx @R0, A 007B EA mov A, R2 007C F8 mov R0, A 007D EF mov A, R7 007E F2 movx @R0, A 007F 7801 mov R0, #0x01 0081 E2 movx A, @R0 0082 F590 mov P1, A 0084 EB mov A, R3 0085 F9 mov R1, A 0086 7800 mov R0, #0x00 0088 7401 mov A, #0x01 008A F2 movx @R0, A 008B 7801 mov R0, #0x01 008D 7402 mov A, #0x02 008F F2 movx @R0, A 0090 7802 mov R0, #0x02 0092 7403 mov A, #0x03 0094 F2 movx @R0, A 0095 7803 mov R0, #0x03 0097 7404 mov A, #0x04 0099 F2 movx @R0, A 009A 7804 mov R0, #0x04 009C 7405 mov A, #0x05 009E F2 movx @R0, A 009F 7805 mov R0, #0x05 00A1 7406 mov A, #0x06 00A3 F2 movx @R0, A 00A4 7806 mov R0, #0x06 00A6 7407 mov A, #0x07 00A8 F2 movx @R0, A 00A9 7807 mov R0, #0x07 00AB 7408 mov A, #0x08 00AD F2 movx @R0, A 00AE 7808 mov R0, #0x08 00B0 7409 mov A, #0x09 00B2 F2 movx @R0, A 00B3 7809 mov R0, #0x09 00B5 740A mov A, #0x0A 00B7 F2 movx @R0, A 00B8 780A mov R0, #0x0A 00BA 740B mov A, #0x0B 00BC F2 movx @R0, A 00BD 780B mov R0, #0x0B 00BF 740C mov A, #0x0C 00C1 F2 movx @R0, A 00C2 780C mov R0, #0x0C 00C4 740D mov A, #0x0D 00C6 F2 movx @R0, A 00C7 780D mov R0, #0x0D 00C9 740E mov A, #0x0E 00CB F2 movx @R0, A 00CC 780E mov R0, #0x0E 00CE 740F mov A, #0x0F 00D0 F2 movx @R0, A 00D1 E3 movx A, @R1 00D2 FF mov R7, A 00D3 EF mov A, R7 00D4 7800 mov R0, #0x00 00D6 F2 movx @R0, A 00D7 EC mov A, R4 00D8 F8 mov R0, A 00D9 EB mov A, R3 00DA F2 movx @R0, A 00DB 7800 mov R0, #0x00 00DD E2 movx A, @R0 00DE FB mov R3, A 00DF EC mov A, R4 00E0 F9 mov R1, A 00E1 7800 mov R0, #0x00 00E3 7400 mov A, #0x00 00E5 F2 movx @R0, A 00E6 7801 mov R0, #0x01 00E8 7400 mov A, #0x00 00EA F2 movx @R0, A 00EB 7802 mov R0, #0x02 00ED 7401 mov A, #0x01 00EF F2 movx @R0, A 00F0 7803 mov R0, #0x03 00F2 7402 mov A, #0x02 00F4 F2 movx @R0, A 00F5 7804 mov R0, #0x04 00F7 7403 mov A, #0x03 00F9 F2 movx @R0, A 00FA 7805 mov R0, #0x05 00FC 7404 mov A, #0x04 00FE F2 movx @R0, A 00FF 7806 mov R0, #0x06 0101 7405 mov A, #0x05 0103 F2 movx @R0, A 0104 7807 mov R0, #0x07 0106 7406 mov A, #0x06 0108 F2 movx @R0, A 0109 7808 mov R0, #0x08 010B 7407 mov A, #0x07 010D F2 movx @R0, A 010E 7809 mov R0, #0x09 0110 7408 mov A, #0x08 0112 F2 movx @R0, A 0113 780A mov R0, #0x0A 0115 7409 mov A, #0x09 0117 F2 movx @R0, A 0118 780B mov R0, #0x0B 011A 740A mov A, #0x0A 011C F2 movx @R0, A 011D 780C mov R0, #0x0C 011F 740B mov A, #0x0B 0121 F2 movx @R0, A 0122 780D mov R0, #0x0D 0124 740C mov A, #0x0C 0126 F2 movx @R0, A 0127 780E mov R0, #0x0E 0129 740D mov A, #0x0D 012B F2 movx @R0, A 012C 780F mov R0, #0x0F 012E 740E mov A, #0x0E 0130 F2 movx @R0, A 0131 E3 movx A, @R1 0132 FF mov R7, A 0133 EF mov A, R7 0134 7800 mov R0, #0x00 0136 F2 movx @R0, A 0137 EC mov A, R4 0138 F8 mov R0, A 0139 F2 movx @R0, A 013A 7800 mov R0, #0x00 013C E2 movx A, @R0 013D FC mov R4, A 013E 020009 ljmp 0x09 ; mov PC, #0x09