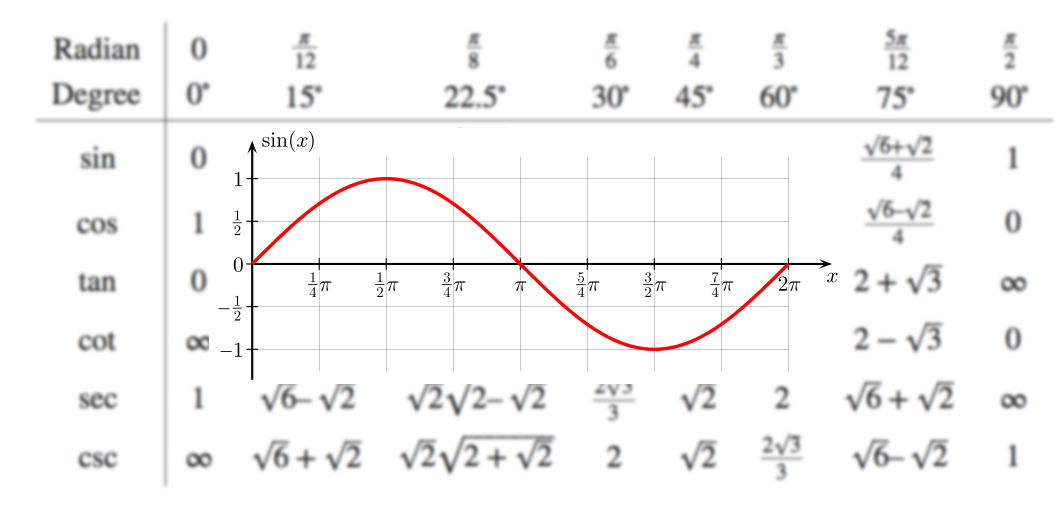
Trigonometric Functions Formulary

This formulary has been created during the online onboarding process at Baden-Wuerttemberg Cooperative State University (DHBW). It is suitable for the related online tests and might be helpful for other people, seeking for formulas in this field of mathematics.

Basics

$$\begin{array}{l} \tan x = \frac{{\sin x}}{{\cos x}}\\ \cot x = {\tan ^{ – 1}}x = \frac{{\cos x}}{{\sin x}} \end{array}$$

Radian and degree conversion
$$\frac{b}{\pi } = \frac{\alpha }{{180}}$$

Sign

Quadrant 1 2 3 4
sin      + + - -
cos      + - - + 
tan      + - + -
cot      + - + -

 Addition theorems

$$\begin{array}{l} \sin \left( {\alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \sin \left( {\alpha – \beta } \right) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \\ \cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \\ \cos \left( {\alpha – \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{array}$$

$$\begin{array}{l} \tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \tan \beta }}\\ \tan \left( {\alpha – \beta } \right) = \frac{{\tan \alpha – \tan \beta }}{{1 + \tan \alpha \tan \beta }}\\ \cot \left( {\alpha + \beta } \right) = \frac{{\cot \alpha \cot \beta – 1}}{{\cot \beta + \cot \alpha }}\\ \cot \left( {\alpha – \beta } \right) = \frac{{\cot \alpha \cot \beta + 1}}{{\cot \beta – \cot \alpha }} \end{array}$$

Relations

$$\begin{array}{l} {\sin ^2}x + {\cos ^2}x = 1\\ {\tan ^2}x + 1 = \frac{1}{{{{\cos }^2}x}}\\ {\cot ^2}x + 1 = \frac{1}{{{{\sin }^2}x}}\\ \cot x = \frac{1}{{\tan x}} \end{array}$$

Sum to product

$$\begin{array}{l} \sin \alpha + \sin \beta = 2\sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}\\ \sin \alpha – \sin \beta = 2\sin \frac{{\alpha – \beta }}{2}\cos \frac{{\alpha + \beta }}{2}\\ \cos \alpha + \cos \beta = 2\cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}\\ \cos \alpha – \cos \beta = – 2\sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha – \beta }}{2} \end{array}$$

Product to sum

$$\begin{array}{l} \sin \alpha \sin \beta = – \frac{1}{2}\left( {\cos \left( {\alpha + \beta } \right) – \cos \left( {\alpha – \beta } \right)} \right)\\ \sin \alpha \cos \beta = \frac{1}{2}\left( {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha – \beta } \right)} \right)\\ \cos \alpha \cos \beta = \frac{1}{2}\left( {\cos \left( {\alpha + \beta } \right) + \cos \left( {\alpha – \beta } \right)} \right) \end{array}$$

Arcus functions

$$\begin{array}{l} \sin \left( {\arcsin a} \right) = \cos \left( {\arccos a} \right) = a,a \in \left[ { – 1,1} \right]\\ \tan \left( {\arctan a} \right) = \cot \left( {{\mathop{\rm arccot}\nolimits} a} \right) = a,a \in\left[ { – \infty,\infty} \right] \end{array}$$

Arcus values $$\begin{array}{l} \alpha = \arcsin a \Leftrightarrow a = \sin \alpha ,\alpha \in \left[ { – \frac{\pi }{2},\frac{\pi }{2}} \right]\\ \beta = \arctan a \Leftrightarrow a = \tan \beta ,\beta \in \left[ {\frac{{ – \pi }}{2},\frac{\pi }{2}} \right]\\ \gamma = \arccos a \Leftrightarrow a = \cos \gamma ,\gamma \in \left[ {0,\pi } \right]\\ \varphi = {\mathop{\rm arccot}\nolimits} a \Leftrightarrow a = \cot \varphi ,\varphi \in \left[ {0,\pi } \right] \end{array}$$

Arcsin of sin $$\arcsin \left( {\sin \alpha } \right) = \left\{ \begin{array}{l} \alpha \bmod 2\pi {\rm{, if }}\left( {\alpha \bmod 2\pi } \right) \in \left[ {0,\frac{\pi }{2}} \right]\\ \left( {\alpha \bmod 2\pi } \right) – 2\pi ,{\rm{ if }}\left( {\alpha \bmod 2\pi } \right) \in \left[ {\frac{{3\pi }}{2},2\pi } \right]\\ \pi – \left( {\alpha \bmod 2\pi } \right),{\rm{ else}} \end{array} \right.$$

Arccos of cos $$\arccos \left( {\cos \alpha } \right) = \left\{ \begin{array}{l} \alpha \bmod 2\pi {\rm{, if }}\left( {\alpha \bmod 2\pi } \right) \in \left[ {0,\pi } \right]\\ \left( { – \alpha } \right)\bmod 2\pi {\rm{, else}} \end{array} \right.$$

Arccot of cot and arctan of tan $$\begin{array}{l} {\mathop{\rm arccot}\nolimits} \left( {\cot \alpha } \right) = \alpha \bmod \pi \\ \arctan \left( {\tan \alpha } \right) = \left\{ \begin{array}{l} \alpha \bmod \pi {\rm{, if }}\left( {\alpha \bmod \pi } \right) \in \left[ {0,\frac{\pi }{2}} \right]\\ \left( {\alpha \bmod \pi } \right) – \pi {\rm{, else}} \end{array} \right. \end{array}$$

Relations between arcus functions $$\begin{array}{l} \arccos a + \arcsin a = \frac{\pi }{2}\\ \arctan a + {\mathop{\rm arccot}\nolimits} a = \frac{\pi }{2} \end{array}$$

Unit circle symmetry

X-axis \[\begin{array}{l} \sin x = – \sin \left( { – x} \right)\\ \cos x = \cos \left( { – x} \right)\\ \tan x = – \tan \left( { – x} \right) \end{array}\]

Y-axis \[\begin{array}{l} \sin x = \sin \left( {\pi – x} \right)\\ \cos x = – \cos \left( {\pi – x} \right)\\ \tan x = – \tan \left( {\pi – x} \right) \end{array}\]

Coordinate origin \[\begin{array}{l} \sin x = – \sin \left( {\pi + x} \right)\\ \cos x = – \cos \left( {\pi + x} \right)\\ \tan x = \tan \left( {\pi + x} \right) \end{array}\]

Angle bisector \[\begin{array}{l} \sin \left( {\frac{\pi }{2} – x} \right) = \cos x\\ \cos \left( {\frac{\pi }{2} – x} \right) = \sin x\\ \tan \left( {\frac{\pi }{2} – x} \right) = \cot x \end{array}\]

Double and half angle

Double angle \[\begin{array}{l} \sin \left( {2\alpha } \right) = 2\sin \alpha \cos \alpha \\ \cos \left( {2\alpha } \right) = 1 – 2{\sin ^2}\alpha \end{array}\]

Double angle with tangent \[\begin{array}{l} \sin \left( {2\alpha } \right) = \frac{{2\tan \alpha }}{{1 + {{\tan }^2}\alpha }}\\ \cos \left( {2\alpha } \right) = \frac{{1 – {{\tan }^2}\alpha }}{{1 + {{\tan }^2}\alpha }}\\ \tan \left( {2\alpha } \right) = \frac{{2\tan \alpha }}{{1 – {{\tan }^2}\alpha }} \end{array}\]

Half angle \[\begin{array}{l} {\sin ^2}\left( {\frac{\alpha }{2}} \right) = \frac{{1 – \cos \alpha }}{2}\\ {\cos ^2}\left( {\frac{\alpha }{2}} \right) = \frac{{1 + \cos \alpha }}{2}\\ \tan \left( {\frac{\alpha }{2}} \right) = \frac{{\sin \alpha }}{{1 + \cos \alpha }}{\rm{, if }}\alpha \in \left[ {0,\pi } \right]\\ = \frac{{\tan \alpha }}{{1 + \sqrt {1 + {{\tan }^2}\alpha } }}{\rm{, if }}\alpha \in \left] { – \frac{\pi }{2},\frac{\pi }{2}} \right[ \end{array}\]

Special values

$$\begin{array}{c|cccccccc}
\begin{matrix}\text{Radian}\\ \text{Degree}\end{matrix} &
\begin{matrix}0\\ 0^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{12}\\ 15^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{8}\\ 22.5^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{6}\\ 30^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{4}\\ 45^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{3}\\ 60^\circ\end{matrix} &
\begin{matrix}\frac{5\pi}{12}\\ 75^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{2}\\ 90^\circ\end{matrix} \\
\hline
\sin &
0 &
\frac{ \sqrt{6} – \sqrt{2} } {4} &
\frac{ \sqrt{2 – \sqrt{2}} } {2} &
\frac{1}{2} &
\frac{\sqrt{2}}{2} &
\frac{\sqrt{3}}{2} &
\frac{ \sqrt{6} + \sqrt{2} } {4} &
1 \\
\cos &
1 &
\frac{\sqrt{6}+\sqrt{2}}{4} &
\frac{ \sqrt{2 + \sqrt{2}} } {2} &
\frac{\sqrt{3}}{2} &
\frac{\sqrt{2}}{2} &
\frac{1}{2} &
\frac{ \sqrt{6} – \sqrt{2}} {4} &
0 \\
\tan &
0 &
2-\sqrt{3} &
\sqrt{2} – 1 &
\frac{\sqrt{3}}{3} &
1 &
\sqrt{3} &
2+\sqrt{3} &
\infty \\
\cot &
\infty &
2+\sqrt{3} &
\sqrt{2} + 1 &
\sqrt{3} &
1 &
\frac{\sqrt{3}}{3} &
2-\sqrt{3} &
0 \\
\sec &
1 &
\sqrt{6} – \sqrt{2} &
\sqrt{2} \sqrt{ 2 – \sqrt{2} } &
\frac{2\sqrt{3}}{3} &
\sqrt{2} &
2 &
\sqrt{6}+\sqrt{2} &
\infty \\
\csc &
\infty &
\sqrt{6}+\sqrt{2} &
\sqrt{2} \sqrt{ 2 + \sqrt{2} } &
2 &
\sqrt{2} &
\frac{2\sqrt{3}}{3} &
\sqrt{6} – \sqrt{2} &
1 \\
\end{array}$$

Differentiation

$$
\begin{align}
\frac{d}{dx}\sin(x) =& \cos(x)\\
\frac{d}{dx}\cos(x) =& -\sin(x)\\
\frac{d}{dx}\tan(x) =& \left(\frac{\sin(x)}{\cos(x)}\right)’ = \frac{\cos^2(x) + \sin^2(x)}{\cos^2(x)} = 1 + \tan^2(x) = \sec^2(x)\\
\frac{d}{dx}\cot(x) =& \left(\frac{\cos(x)}{\sin(x)}\right)’ = \frac{-\sin^2(x) – \cos^2(x)}{\sin^2(x)} = -(1+\cot^2(x)) = -\csc^2(x)\\
\frac{d}{dx}\sec(x) =& \left(\frac{1}{\cos(x)}\right)’ = \frac{\sin(x)}{\cos^2(x)} = \frac{1}{\cos(x)} \cdot \frac{\sin(x)}{\cos(x)} = \sec(x)\tan(x)\\
\frac{d}{dx}\csc(x) =& \left(\frac{1}{\sin(x)}\right)’ = -\frac{\cos(x)}{\sin^2(x)} = -\frac{1}{\sin(x)} \cdot \frac{\cos(x)}{\sin(x)} = -\csc(x)\cot(x)\\
\frac{d}{dx}\arcsin(x) =& \frac{1}{\sqrt{1-x^2}}\\
\frac{d}{dx}\arccos(x) =& \frac{-1}{\sqrt{1-x^2}}\\
\frac{d}{dx}\arctan(x) =& \frac{1}{1+x^2}\\
\frac{d}{dx}\mbox{arccot}(x) =& \frac{-1}{1+x^2}\\
\frac{d}{dx}\mbox{arcsec}(x) =& \frac{1}{|x|\sqrt{x^2-1}}\\
\frac{d}{dx}\mbox{arccsc}(x) =& \frac{-1}{|x|\sqrt{x^2-1}}
\end{align}$$